5.3 KiB
I fluidi hanno una pressione che si distribuisce su tutta la superfice a contatto.
Fluidi Ideali
Un fluido è detto ideale se rispetta le seguenti condizioni:
- è un fluido
- è incomprimibile
- è privo di attrito
Equilibrio dei Fluidi
La legge di Stevino
"In un liquido in equilibrio, la differenza di pressione
p-p_0tra un punto a profonditàhe la superfice è direttamente proporzionale ahe non dipende dalla forma del recipiente"
La legge di Stevino vale per i liquidi, ovvero fluidi incomprimibili di densità d costante e indipendente dalla profondità h.
La legge è espressa dalla formula
p=p_0+dghin cui g è l'accelerazione di gravità, p_0 è la pressione sulla superfice del liquido (= 1 atm quando all'aria) ed h è la profondità.
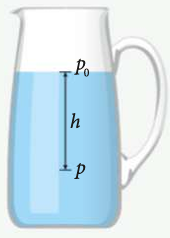
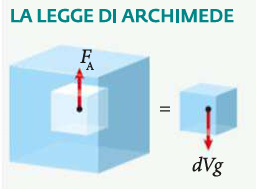
La legge di Archimede
Su un corpo immerso in un fluido, la differenza di pressione tra gli stati a profondità diverse crea una forza (\overrightarrow{F_A}) verso l'alto, chiamata spinta di Archimede.
La forza è data dalla formula
F_A=Vdg
analisi dimensionale
N=\frac{m^3kgm}{m^3*s^2}
(aka: "Vedi Di Galleggiare"), in questo caso V è il "volume d'acqua spostato"="il volume immerso", g è la gravità e d è la densità del fluido.
Il galleggiamento
Un corpo:
- affonda se il peso è maggiore della forza di Archimede
- rimane stabile il peso è uguale alla forza di Archimede
- galleggia se il peso è minore della forza di Archimede ovvero se la densità dell'oggetto è maggiore, uguale o minore di quella del fluido.
La corrente
Una corrente è un movimento ordinato di un liquido o di un gas. La sede di una corrente è il suo condotto.
Per misurare la corrente si usa la portata.
Una corrente si dice ==stazionaria== quando la velocità del fluido è costante nel tempo in ogni punto.
La portata
La portata
qdi una corrente che attraversa una sezione trasversale del condotto è il rapporto tra il volume di fluido\Delta Vche oltrepassa la sezione in un intervallo di tempo\Delta te l'intervallo di tempo stesso\Delta t
q=\frac{\Delta V}{\Delta t}
analisi dimensionale
q=\frac{m^3}{s}
se la velocità è uguale in tutti i punti della sezione allora
q=Sv
dove S è l'area della sezione e v è la velocità.
Se la velocità è uguale e se il fluido è un liquido incomprimibile si può applicare
S_A v_A = S_B v_Bovvero dice che:
- la portata non varia con la sezione trasversale in uno stesso tubo
- l'area e la velocità sono inversamente proporzionali
Condotti irregolari
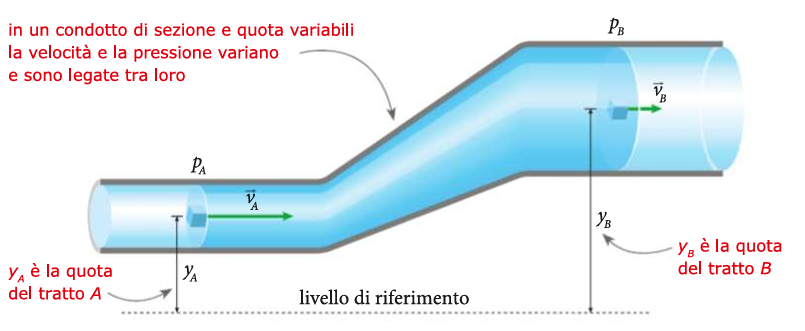In un condotto come il precedente, dove cambia grandezza e dimensione, rimane fisso durante tutto il condotto il valore di questa formula:
p + \frac{1}{2}dv^2 + dgy
in cui:
pè la pressionedè la densità del liquidovè la velocitàgè la accelerazione di gravitàyè la quota da un livello di riferimento prefissato funziona solo con i Fluidi Ideali, e ne descrive le correnti stazionarie.
La legge di Torricelli
Un recipiente aperto ha un foro a profondità h l'acqua esce alla velocità specificata dalla formula v=\sqrt{2gh}
Preparazione per la verifica
| Formula | Utilizzo |
|---|---|
q=\frac{\Delta V}{\Delta t} |
q è per calcolare la portata |
q=Sv |
quando la velocità è uguale in tutto il fluido |
S_A v_A = S_B v_B |
con un fluido incomprimibile nello stesso \Delta t e la velocità è uguale in tutto il fluido |
p + \frac{1}{2}dv^2 + dgy = \text{costante} |
rimane invariato nello stesso condotto, con Fluidi Ideali |
v=\sqrt{2gh} |
velocità di caduta in da un buco di un contenitore aperto |
- Cos'è una corrente?
la corrente è un movimento ordinato di un fluido e passa dentro un condotto.
- Cos'è la portata? Fornisci la sua formula generale e spiegane il significato.
q=\frac{\Delta V}{\Delta t}la portata misura la quantità di fluido (in\frac{m^3}{s}) che passa per una determinata sezione trasversale
- Quali sono le ipotesi per cui vale la formula
q=Sv?
la velocità è la stessa in tutti i punti della sezione trasversale da cui è stata presa l'area è
S
- Quando si può dire che una corrente è stazionaria?
quando rimane invariata nel tempo
- Enuncia l'equazione di continuità e spiegane il significato.
S_A v_A = S_B v_B, dice che "la portata è uniforme lungo il condotto" (la portata non varia al variare della sezione trasversale) e che "l'area della sezione e la velocità sono inversamente proporzionali"